Alexander Kuklev

“Новые Основания” и Новые Основания

Годовщине изгнания из канторианского рая посвещается

В 1884 году в работе «Die Grundlagen der Arithmetik» («Обоснования арифметики») великий логик Gottlob Frege показал, что натуральные числа и законы арифметики неявно содержатся уже в самой логике, безо всякой отсылки к эмпирическим соображениям. Для строгого доказательства предстояло разработать мощную формальную систему математической логики, что заняло у него без малого 20 лет. Результат превзошёл изначальную задумку: через редукцию к чистой логике были обоснованы не только сами натуральные числа и законы арифметики, но и множества натуральных чисел вместе с законами теории множеств, и множества этих множеств, и так далее. По всему выходило будто чистая логика даёт обоснование конструкций достаточно мощных, чтобы служить общей базой для всей математики! Формальная система Фреге совмещала элегантность, минимализм и невероятную мощь, пока не рассыпалась в одночасье — философ и математик Bertrand Russell нашёл в системе формальное противоречие.

В 1937 философ и математик Willard Quine предложил логическую систему NF (от «New Foundations for Mathematical Logic»), которая была очень близка по построению к исходной системе Фреге, но избегала обнаруженного противоречия. На деле NF оказалась слаба и неудобна в качестве общематематической базы, хотя и решала исходную задачу Фреге по обоснованию арифметики через редукцию к чистой логике^[Tu12]. Впрочем, как выяснилось в 1984 году, с обоснованием арифметики справляется и куда более заурядная логика второго порядка. Тем не менее, у NF нашлась уникальная ниша: NF и её производные являются единственными известными логическими системами, пригодными для рассуждения об всеобъемлющих самосодержащих структурах, таких как множество всех множеств и категория всех категорий.

Разумеется, у математиков сразу возникли вопросы о непротиворечивости NF. Целый ряд результатов заставлял усомниться в её непротиворечивости, а все попытки доказать её относительную непротиворечивость десятилетиями оказывались бесплодными. И вот, спустя без малого девяносто лет, в этом вопросе наконец была поставлена точка. Доказательство непротиворечивости, которое предложил Randall Holmes в 2010, в этом апреле было успешно формализовано и верифицировано в Lean его аспиранткой Sky Wilshaw^[HW24].

Доказательство непротиворечивости NF — отличный повод поговорить подробнее о том, что такое теория множеств, какое отношение она имеет к основаниям математики, и какова современная точка зрения на эти вопросы.

Аксиоматические теории и исчисление предикатов

Прежде чем мы сможем предметно обсудить идею Фреге и основания математики в целом, необходимо напомнить о том, что такое аксиматические теории и логика предикатов.

Около 300 года до н.э. греческий философ и математик Евклид Александрийский написал монографию «Начала» (Στοιχεῖα), где он демонстрирует на огромном количестве примеров, что всевозможные свойства геометрических фигур, выводимы при помощи законов логики из небольшого набора постулатов (“аксиом”). Так родилось понятие аксиоматической теории.

Любая аксиоматическая теория определяется своим языком — языком, на котором формулируются её утверждения, — и набором записанных на этом языке постулатов, с использованием которых доказываются или опровергаются утверждения. Язык всякой аксиоматической теории состоит из:

• набора специфичных для данной теории понятий:
  • разновидностей упоминаемых в постулатах сущностей — например, точки, линии и длины,
  • отношений между этими сущностями — например, параллельность линий
• общей для всех теорий базы:
  • отношения равенства (=),
  • логических операторов «и», «или», «следовательно», «не»,
  • кванторов «существует такой х, что φ[x]» и «для любого х выполняется φ[x]», где φ[x] — произвольный логический предикат, то есть утверждение с параметром.

Словарик понятий, принятых в качестве базовых, называется сигнатурой теории, а общелогическая база вместе с правилами логического вывода называется исчислением предикатов.

Именно Готтлоб Фреге дал первую исчерпывающую формализацию исчисления предикатов^[Fr1879].

Аксиоматическая теория логических предикатов (= наивная теория множеств)

У всякой аксиоматической теории есть своя предметная область. Эвклидова геометрия — аксиоматическая теория фигур на плоскости. Арифметика Пеано — аксиоматическая теория натуральных чисел. Возможна ли аксиоматическая теория, предметной областью которой является сама подлежащая логика?

Логическая система, предложенная Фреге в 1884 году — именно такая теория: аксиоматическая теория, предметом рассмотрения которой является сами логические предикаты этой теории. Эта теория имеет особый эпистемический (“философский”) статус, т.к. в отличие от других аксиоматических теорий, она не аппелирует ни к какой внешней предметной области для обоснования своих постулатов.

Напомним, что логический предикат это выразимое на языке данной теории утверждение φ[x] c параметром. Говоря современным языком, идея Фреге состояла в том, чтобы каждый логический предикат (элемент синтаксиса теории) представлялся объектом теории (элементом её семантики). Чтобы как-то отличать первые от последних, объекты теории (“отражения логических предикатов”) называются множествами, а единственное отношение в сигнатуре предлагаемой теории называется отношением принадлежности: x ∈ S «множество x является элементом множества S». Будем говорить, что множество S представляет предикат φ[x], если x ∈ S ⇔ φ[x], то есть если множество S содержит в точности те же множества, для которых выполняется предикат φ[x].

Аксиоматическая теория логических предикатов состоит из общих для всех аксиоматических теорий законов логики и принципа Фреге, гласящего что для каждого предиката существует представляющее его множество, однозначно определяемое предикатом, то есть бесконечного семейства постулатов вида
　∃!(S) x ∈ S ⇔ φ[x]
— по одному для каждого выразимого на языке теории предиката φ[x].

Эту теорию и её фрагменты, в которых принцип Фреге выполняется с теми или иными ограничениями, называют фундаментальными теориями множеств.

Понятие множества в фундаментальных теориях множеств

При первом знакомстве, множества обычно изображают как кружочки, содержащие буквы, цифры или точки. В формулировках задач и теорем часто упоминают конечные или бесконечные множества чисел, множества точек, множества решений каких-нибудь уравнений — конкретные множества, совокупности каких-то наперёд определённых объектов без учёта порядка и повторений. Пионер теории множеств Georg Cantor изначально также исследовал конкретные множества — множества вещественных чисел, возникавшие в контексте его работ по тригонометрическим рядам.

В фундаментальных теориях множеств речь не про них. Принцип Фреге определяет “множества” как объектификацию логических предикатов. А коль скоро “множества” суть объекты этой теории, то логические предикаты описывают свойства множеств. Таким образом, множества в фундаментальных теориях множеств это объектификация предикатов о самих себе — не множества каких-то наперёд заданных объектов, а “множества сами по себе”. Они напоминают конкретные множества тем, что их тоже можно рассматривать как “совокупности объектов без учёта порядка и повторений”, но их элементы не какие-то объекты самостоятельной природы, а другие такие же множества.

Но как же себе их вообще представить, если нет никаких “первичных элементов”? На помощь приходит пустое множество ∅, которое можно сконструировать безо всяких первичных элементов. Используя его в качестве элемента, можно построить множество {∅} — множество, содержащее пустое множество и только его. Дальше можно построить множество {∅, {∅}}, элементами которого являются два приведённых прежде множества: пустое и оболочку пустого. Продолжая в том же духе, можно сконструировать множества любого конечного размера.

Предмет рассмотрения фундаментальных теорий множеств — такие вот абстрактные множества, довольно искуственные и причудливые математические объекты. Но они отождествляются с логическими предикатами о самих себе, что как будто делает их объектами универсальной, чисто логической природы.

Логицизм

Ещё раз подчеркнём, что наивная теория множеств, это не эмпирическая теория, аксиоматизирующая эмпирическое понятие множества, а чистая логическая система, не аппелирующая ни к какой внешней предметной области, и изучающая объекты универсальной, чисто логической природы — автореферрентные логические предикаты. И тем не менее мы можем сконструировать в рамках этой теории “из ничего“ объекты любых конечных размеров:
　∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}, …

Язык теории множеств позволяет описать концепцию одноэлементности: множество S одноэлементное, если существует такой элемент a ∈ S, что любой другой элемент x ∈ S ему равен:
　∃(a ∈ S) ∀(x ∈ S) x = a.

Аналогично мы можем описать двуэлементность — множество S двуэлементное, если существуют такие неравные между собой элементы a ∈ S и b ∈ S, что любой другой элемент x ∈ S равен a или b:
　∃(a b ∈ S, a ≠ b) ∀(x ∈ S) (x = a ∨ x = b)

Естественный способ концептуализации понятия натурального числа в терминах чистой логики — отождествлять натуральное число n с концепцией n-элементности, т.е. число n это множество всех n-элементных множеств. Благодаря конструкции из первого абзаца мы знаем, что все натуральные числа суть непустые множества, и различные натуральные числа не равны как множества. Продолжая в том же духе, мы можем также определить множество всех натуральных чисел, операции сложения и умножения на нём и вывести все аксиомы арифметики из чистой логики, что известно как теорема Фреге.

Сведение арифметики к логике стало отправной точкой и одновременно парадным результатом логицизма — программы сведению максимально широкого круга математических понятий чистой логике. Однако дальнейшие успехи логицизма оказались весьма скромны — кроме натуральных чисел лишь очень редкие математические понятия можно столь же естественно понимать как множества: собственно множества натуральных чисел, индуктивные ординалы, да ещё ряд понятий из области теоретико-множественной топологии и теории игр. В большинстве же случаев естественного способа мыслить об объектах определённого типа, как о множествах, всё же нет. Характерным антипримером тут является понятие упорядоченной пары. Уже из соображений симметрии ясно, что не может существовать естественного способа думать об упорядоченных парах, как о множествах. Разумеется, упорядоченные пары можно кодировать множествами, но выбор способа кодирования является произвольным решением. Тем не менее, выбрав фиксированный способ кодирования, мы сводим упорядоченные пары и операции над ними к множествам и операциям над ними (и таким образом в конечном итоге как будто к чистой логике) — это называется теоретико-множественным редукционизмом, ослабленной формой логицизма.

Теоретико-множественный редукционизм

Кроме эвклидовой геометрии имеются сотни других важных аксиоматических теорий, начиная с арифметики, вещественного анализа, и т.д. Однако, все математические области взаимосвязаны, и чтобы заниматься математикой в комплексе нужна какая-то общая база, например “аксиоматическая теория математических кирпичей”, в которую отображаются отдельные аксиоматические теории.

В процессе логицистского обоснования арифметики, Фреге понял, что наивная теория множеств — идеальный кандидат на роль такой теории. За несколько лет до того, в той самой работе, где Фреге впервые исчерпывающе формализовал исчисление предикатов^[Fr1879]. В наивной теории множеств объекты и есть предикаты теории, так что она автоматически содержит исчисление предикатов второго (и третьего, и четвертого,…) порядка. Это свойство вкупе с возможностью моделировать натуральные числа открывает путь к моделированию практически любых математических сущностей. Через подмножества натуральных чисел можно кодировать их последовательности, вещественные числа, последовательности вещественных чисел, функции на вещественных числах и т.д.

В фундаментальные теории множеств можно транслировать любые другие аксиоматические теории, в том же духе как компьютерные программы можно транслировать с высокоуровневых языков на низкоуровневый машинный язык. При трансляции теряется различимость разнородных объектов (скажем, какое-нибудь вещественное число может случайно кодироваться тем же множеством, что и какая-нибудь последовательность натуральных чисел) и нарушается принцип структурной эквивалентности (неразличимые объекты очень часто транслируются в различные множества), но не смотря на это на протяжении целого столетия многие математики идентифицировали математические объекты с их теоретико-множественной реализацией.

Изгнание из рая

Наивная теория множеств казалась философски-математическим раем: из чистой логики, применяемой к самой себе, выводится арифметика и строится общая база для всех разделов математики. Изгнание из рая свершилось 16 июня 1902. В этот день Бертран Рассел написал письмо Готтлобу Фреге, который как раз готовил к печати второй том своей монографии. “There is just one point where I have encountered a difficulty” — писал он:
Принцип Фреге позволяет сконструировать множество {x | x ∉ x} всех множеств, не содержащих самих себя. Но если оно существует, то принадлежит ли оно само себе? На этот вопрос невозможен ни положительный, ни отрицательный ответ. Единственный выход — признать, что такое множество не может существовать.

Философски-математический рай развалился как карточный домик и математика вошла в глубокий кризис оснований, радикально изменивший её лицо. Шок был столь велик, что и саму теорему Фреге (о возможности обосновать арифметику логикой) сгоряча посчитали ошибочной и реабилитировали лишь спустя 80 лет.

Оказавшийся недопустимым принцип Фреге позже назвали неограниченным принципом выделения. Чтобы избежать противоречий, его нужно тем или иным способом ограничить так, чтобы из него не следовало существование паталогических автореферрентных объектов типа {x | x ∉ x}. Начался поиск непротиворечивых фрагментов аксиоматической теории предикатов, которые бы годились для использования в качестве общематематических оснований. Ведь никаких других идей, что можно было бы использовать в качестве общематематических оснований, на тот момент не было.

Стандартная теория множеств

Принцип Фреге в общем виде приводит к противоречиям, но можно выделить допустимые частные случаи. Таким частным случаем являются иерархические множества, которые мы определим в следующем абзаце. Ограничивая рассмотрение иерархическими множествами можно выделить стандартную теорию множеств, используемую в качестве общематематических оснований уже более столетия, до недавнего времени — де-факто безальтернативно.

Чтобы понять иерархические множества, рассмотим следующую операцию: пусть 𝓟(S) множество всех ограничений множества S предикатами, то есть множество всех подмножеств множества S, включая само S — множество 𝓟(S) содержит S в качестве элемента, так как S = «подмножество всех элементов S» = { x ∈ S | x = x }, ограничение S предикатом, заведомо выполняющимся для всех его элементов. У пустого множества ∅ в точности одно подмножество — оно само. Стало быть 𝓟(∅) = {∅}. Применим 𝓟 к результату: 𝓟²(∅) = 𝓟{∅} = {∅, {∅}}, и продолжим итерировать:

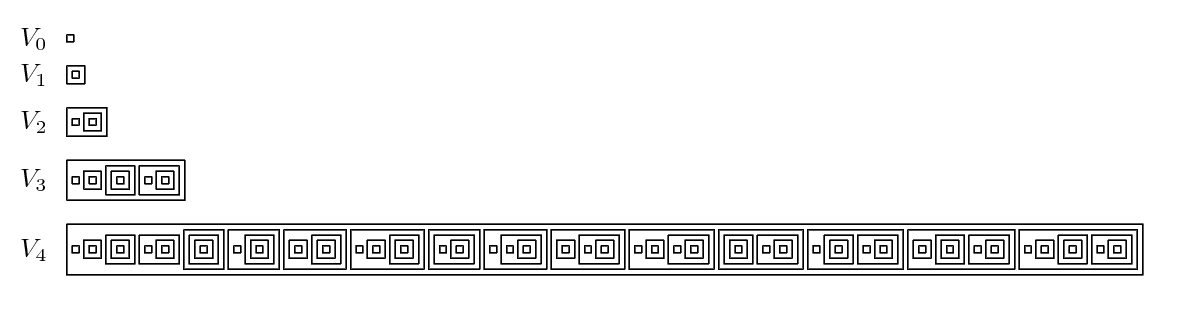
Выходит растущее семейство конечных множеств, а в пределе
　∅ ⊊ 𝓟(∅) ⊊ 𝓟²(∅) ⊊ ··· 𝓟^ω(∅)
получается в точности множество всех иерархически конечных множеств — конечных множеств конечной глубины, элементы которых тоже иерархически конечны. Само же множество 𝓟^ω(∅) содержит n-кратные оболочки пустого множества ∅ⁿ = {..{∅}..} для всякого конечного n, и поэтому является множеством неограниченной глубины. И тем не менее, для 𝓟^ω(∅) невозможно написать бесконечную цепочку вложений принадлежности 𝓟^ω(∅) ∋ x ∋ y ∋ ···, т.к. фиксируя x мы выбираем какой-то конкретный элемент 𝓟^ω(∅), а он в свою очередь уже множество какой-то конечной глубины n, и цепочка принадлежности вправо от него упирается в пустое множество ··· ∋ ∅ максимум через n шагов. Множества, для которых цепочка принадлежности всегда рано или поздно упирается в ∅ мы будем называть иерархическими множествами. Это условие эквивалентно возможности проведения доказательств по-индукции вдоль отношения (∋). Операция 𝓟 сохраняет иерархичность, т.е. если R = 𝓟(Q) и Q иерархично, то R тоже иерархично.

Элементы множества 𝓟^ω(∅) — иерархически конечные множества — можно без труда пронумеровать, так что подмножества 𝓟^ω(∅) можно описывать как множества натуральных чисел (такие как “множество чётных положительных чисел”, “множество простых чисел” и т.д.), очень естественные математические объекты. Это даёт повод считать, что операцию 𝓟 допустимо применять не только к иерархически конечным (т.е. входящих в 𝓟^ω(∅)) множествам, но и к самому множеству 𝓟^ω(∅). Множества натуральных чисел в свою очередь можно отождествить с вещественными числами, а множества вещественных чисел тоже очень естественные математические объекты. Их мы в свою очередь можем отождествить с функциями на вещественных числах, а множества таких функций опять же естественные математические объекты. Таким образом выходит что множества 𝓟ⁿ(𝓟^ω(∅)) естественно возникают в “обыкновенной” математике.

Стандартная теория множеств ZF (Zermelo-Fraenkel set theory) получается в предположении, что 𝓟 допустимо применять ко множествам, получаемым из ∅ последовательным применением операции 𝓟 и взятием пределов растущих семейств таких множеств. Выясняется, что из этого предположения автоматически следует, что “сверхдлинная бесконечная последовательность” применений 𝓟 к пустому множеству рано или поздно накрывает каждое иерархическое множество. Таким образом предметом рассмотрения стандартной теории множеств являются в точности все иерархические множества.

Парадокс Рассела и все известные родственные ему парадоксы основываются на использовании ‘проблемных’ множеств, содержащих сами себя. Не все содержащие себя множества ‘проблемные’, но если хочется надёжной математической базы, то лучше запретить слишком много, чем слишком мало. Ограничение области рассмотрения иерархическими множествами именно такое решение: исключая из рассмотрения множества, допускающие бесконечные вправо цепочки принадлежности
　x ∋ y ∋ z ∋ ···
мы как раз исключаем любые множества, прямо или опосредованно содержащие сами себя, такие как множество всех множеств U ∋ U (“абсолютный универсум”) и одноэлементное самосодержащее множество Q = {Q} (“атом Куайна”). То, что в результате такого ограничения остаются в точности множества, допускающие построение снизу начиная с пустого множества — приятный сюрприз, указывающий на состоятельность такого подхода.

В отличие от наивной теории множеств, в стандартной теории множеств множества отождествляются с предикатами на множествах уже не точно. Всё ещё верно, что всякое множество S однозначно определяется предикатом ( ∈ S), но не все предикаты представимы множествами. Кроме того, теряется уникальная стройность аксиом наивной теории множеств. Однако именно этот подход оказался успешен и крайне продуктивен. В частности, состоятельность аксиоматических теорий неизменно доказывается путём построения теоретикомножественных моделей в стандартной теории множеств или одном из её общепринятых расширений.

Использование стандартной теории множеств в этом качестве далеко не историческая случайность. Недавно удалось^[Pa19] выделить теорию H_<ω — финитистское ядро стандартной теории множеств, где выводимо лишь существование 𝓟ⁿ(∅) для каждого конечного n, но всякая её конечная подтеория, то есть всякий конечный набор выводимых в ней утверждений, имеет конечную модель. В частности это означает, что в ней нельзя доказать ни существования бесконечного множества, ни существования неограниченно растущей в каком бы то ни было смысле операции. H_<ω — уникальная теория, осознающая собственную непротиворечивость. Всякое математическое доказательство обязано быть конечной длины, и поэтому может использовать лишь конечное число аксиом. Значит всякое доказуемое в ней утверждение H_<ω выводимо её конечной подтеории, непротиворечивость которой следует из наличия модели, а любые конечные теоретикомножественные модели можно построить в H_<ω, что замыкает круг. Этот аргумент может быть превращён в строгое формальное доказательство непротиворечивости H_<ω при помощи H_<ω, что и называется «H_<ω осознаёт свою непротиворечивость». Будучи финитистской H_<ω избегает проклятия знаменитой теоремы Гёделя, исключающей возможность осознания собственной непротиворечивости для более сильных теорий.

Добавляя к H_<ω постулат о существовании внутренней модели H_<ω (множества 𝓟^ω(∅) всех иерархически конечных множеств) мы получим теорию, равномощную элементарной арифметике. Используя более сильные постулаты о существовании внутренних моделей мы можем получить стандартную теорию множеств ZF и её общепринятые расширения, используемые для моделлирования других теорий.

Ограниченный принцип Фреге

У стандартной теории множеств существует масса эквивалентных аксиоматизаций, каждая из которых проливает свет на какой-то свой аспект. Выше показан подход, акцентирующий внимание на том, что стандартная теория множеств рассматривает только иерархические множества, и они оказываются как раз теми множествами, которые можно построить снизу-вверх итерируя операцию 𝓟. Стандартная аксиоматизация более конкретна — она описывает типовые способы построения множеств, используемые на практике, такие как например образование неупорядоченных и упорядоченных пар. Есть аксиоматизации, конкретные следствия которых напротив очень неочевидны на превый взгляд, но зато близкие к наивной теории множеств наличием элегантного принципа, из которого следует всё остальное. Таковы аксиоматизация фон Неймана-Гёделя-Бернайса (NBG) и аксиоматизация Аккермана (A*/V).

Обе они позволяют говорить не только о “конкретных множествах”, но и о “воображаемых множествах”, и постулируется ослабленный принцип Фреге: любой теоретикомножественный предикат определяет воображаемое множество конкретных множеств, удовлетворяющих этому предикату. В том числе имеется воображаемое множество V всех конкретных множеств. Защитой от парадокса Рассела является тот факт, что в обеих этих теориях V ∉ V.

Критерии, когда воображаемое множество оказывается конкретным в NBG и A*/V разные:

• В NBG множество конкретное в точности если оно не биективно V (“limitation of size”).
• В A*/V предикат φ задаёт конкретное множество в точности если все кванторы в нём могут быть ограничены на V без изменения смысла:

      φ ⇔ φᵛ
  –––––—––––––––––––––
   {x ∈ V | φ(x)} ∈ V
  

В обоих случаях оказывается что конкретные множества это в точности иерархические множества стандартной теории множеств, и про них можно доказать в точности те же факты, которые можно доказать в стандартной теории множеств. В части воображаемых множеств NBG и A*/V различаются. Язык обеих достаточно выразителен, чтобы дать определение больших конкретных категорий (таких как категория всех групп, категория всех колец или категория всех топологических пространств), но дать определение функтора между большими конкретными категориями можно дать лишь в A*/V, т.к. в NBG элементами воображаемых множеств могут являться только конкретные множества. В целом теория A*/V предоставляет отличную онтологическую базу для теории категорий^[Mu2001], однако не позволяет доказывать нетривиальные факты про большие категории, если не дополнить её принципом рефлексии^[Shu2008]. Отметим, однако, что и в этом случае у нас не появляется циркулярности. Категория больших конкретных категорий сама не является конкретной и потому не входит в саму себя.

Система NF

Выше мы рассказали один из способов выделить непротиворечивый фрагмент системы Фреге — стандартную теорию множеств. Альтернативный подход — разработанная в 1937 философом и математиком Ўиллардом Кўайном система NF, название которой происходит от названия статьи New Foundations for Mathematical Logic, где эта система описывается. В то время как стандартная теория множеств мотивирована поиском “надежной почвы под ногами”, NF это попытка ”запретить только заведомо ядовитое“. Как и фрегеанская теория множеств, эта система состоит из логики предикатов с одним единственным семейством аксиом — принципом выделения Фреге, но уже не для всех предикатов, а лишь для их части. Представимыми через множества постулируются не все предикаты, а лишь стратифицируемые, где стратифицируемость — синтаксическое свойство логической формулы, защищающее от паталогических случаев.

Ряд результатов заставлял усомниться в непротиворечивости NF, поэтому чтобы математики всерьёз занимались NF, было необходимо было показать её непротиворечивость относительно стаднартной теории множеств, чего не удавалось сделать на протяжении более чем 80 лет. В районе 2010 года математик Randall Holmes выложил препринт такого доказательства, однако никто не был готов делать peer review этой статьи — сам же автор во введении употребляет фразу ‘insanely involved with nasty bookkeeping’ (безумно насыщено монструозной бухгалтерией) в отношении своего доказательства. И вот вместо того чтобы ждать пока кто-то снизойдёт до проверки этого монстуруозного доказательства, они с аспиранткой Sky Wilshaw взяли и формализовали доказательство, так что его проверил компьютер. https://www.logicmatters.net/…/21/nf-really-is-consistent/ Наконец-то стало можно экспериментировать с NF без опасений.

На практике NF оказалась не такой уж удобной, но очень интересной философски. В частности, количественные числа там можно определить как завещал Фреге — как классы эквивалентности множеств по взаимно-однозначной сопостовляемости. В стандартной теории множеств приходится проявлять произвол и выбирать какой-то конкретный способ кодирования натуральных чисел множествами — один из нескольких довольно естественных. В NF число n это просто совокупность всех n-элементных множеств, объектификация самого понятия n-элементности. NF позяволяет показать существование множества натуральных чисел, а в месте с ним множества всех его подмножеств (= вещественных чисел), множества их подмножеств и так далее. Иерархические множества, не входящие в 𝓟ⁿ(𝓟^ω(∅)) для конечных n, в NF смоделировать уже не получится. Таким образом с т.з. моделирующей мощности NF как раз достаточна для “обыкновенной математики”, но гораздо слабее стандартной теории множеств. При этом NF способна на то, на что недоступно в стандартной теории множеств.

NF — уникальная система, допускающая всеобъемлющие структуры, содержащие сами себя:

• множество всех множеств (само по себе являющееся множеством, и потому включающее себя);
• множество всех ординалов (само по себе являющееся ординалом, и потому включающее себя);
• категорию всех категорий.

Кроме NF и её вариантов вообще не существует никаких известных способов рассуждать о всеобъемлющих самосодержащий структурах. Обсуждение парадокса Кантора без NF походит на то, как древние греки рассуждали о присосках и насосах, объясняя механизм их действия через умозрительный принцип “природа боится пустоты”. Используя подход NF мы можем в каком-то смысле “обнаружить атмосферное давление”.

Парадокс Кантора

Какими по размеру бывают множества? Конечно они могут быть конечными, и тогда их размер записывается натуральным числом. А есть бесконечное множество натуральных чисел и другие бесконечные множества, элементы которых можно пересчитать натуральными числами. Неискушенный человек подумает, что все бесконечные множества таковы. Собственно все так и думали, пока в 1891 году Кантор доказал свою знаменитую теорему: какое бы множество S мы ни взяли, множество ℘(S) всех его подмножеств будет строго больше. В частности натуральных чисел недостаточно, чтобы пронумеровать все вещественные числа — множество вещественных чисел строго больше, оно несчётно бесконечное. А теперь рассмотрим множество вообще всех множеств M. Оно самое большое из всех возможных, так как все все другие множества являются его подмножествами и одновременно элементами. Оно равно своему множеству подмножеств M = ℘(S). Но это противоречит теореме Кантора! Стандартное решение проблемы — вообще исключить из рассмотрение множество всех множеств M, ведь оно содержит само себя и этим “паталогично”. А в NF выходит так, что стандартное доказательство теоремы Кантора не работает из-за синтаксических ограничений. Там теорема Кантора выполняется уже не для любых множеств, а только для некоторых, и множество всех множеств к таковым не относится.

Вместо заключения: настоящие новые основания

«Исчисление концепций — подобный арифметическому формульный язык чистого мышления» — так называлась эпохальная статья Фреге 1879 года, первая исчерпывающая формализация исчисления предикатов, и, вероятно, вообще первая работа вводящая само понятие формализованного языка и формальной системы.

К новым подходам в основаниях математики привела неожиданная конвергенция идей из таких бесконечно далёких на первый взгляд областей как теория вычислений, теории языков программирования, теория категорий и алгебраическая топология — областей, ни одной из которых ещё не существовало во времена Фреге. Хоть работы ещё и не завершены, сейчас отчётливо видны контуры высше-категорного исчисления построений^[GWB24], где под “построениями” понимается совместное обобщение геометрических построений циркулем и линейкой, теоретикомножественных построений, алгоритов и доказательств. Высшекатегорное исчисление построений — подобный арифметическому формульный язык высшей теории категорий, а ещё оно одновременно является обобщением исчисления предикатов и формальной системой естественной дедукции (“записи доказательств“) для него. Кроме того, высшекатегорное исчисление построений одновременно является выразительным функциональным языком программирования, который в частности позволяет удобочитаемым образом описывать преобразования выражений заданного синтаксиса — многочленов, алгебраических, арифметических или теоретикомножественных утверждений, выражений фиксированного языка программирования и т.д.

Такая формальная система позволяет перейти в основаниях математики от редукционистского подхода, во многом популяризованному тем же Фреге, к подходу структуралистскому. Редукционизм, то есть трансляция на низкоуровневый язык высокоуровневых объектов, такие как геометрические фигуры, группы симметрий, матрицы или вещественные числа, превращает их в кашу из множеств в математике или кашу из битов в программировании, с которой очень неудобно работать напрямую, что приводит к непрозрачным соглашениям и неявным допущениям. Устранение трансляции делает математическую работу одновременно более прозрачной концептуально, и более удобной практически. Исчисление построений даёт возможность работать на одном общем языке и в рамках одной общей системы со всеми разделами математики напрямую, без трансляции в какую-либо “теорию математических кирпичей”.

Вместо того чтобы транслировать языки аксиоматических теорий в теоретикомножественный язык и моделировать объекты этих теорий иерархическими множествами, в рамках исчисления построений мы можем рассматривать аксиоматические теории как самостоятельные сущности и вводить их объекты и операции как самостоятельные, отдельные объекты и операции, мирно сосуществующие с объектами и операциями других теорий и базовыми объектами и операциями самой подлежащей формальной системы. Не только объекты и операции, но также утверждения и доказательства всякой аксиоматической теории становятся объектами — синтаксическими объектами, для которых можно определять преобразования рекурсивно в частности производить доказательства по индукции.

Результат о непротиворечивости NF раскрывает новые возможности в отношении построения элегантных консервативных расширений исчислении построений, позволяющих рассуждать о всеъобъемлющих объектах. Стандартная теория множеств в рамках структуралистского подхода перестаёт использоваться в качестве “аксиоматической теории общематематических кирпичей”, но не уходит со сцены как нечто устаревшее. С одной стороны стандартные теории множеств остаются субстратом для построения моделей других теорий и измерения их моделлирующей силы, а с другой остаются самостоятельной и развивающейся областю математики, где не смотря на полтора века развития, ничуть не реже чем во времена Кантора и происходят открытия и кипит жизнь.